Shape and Space
Symmetry:
- The quality of being made up of exactly similar parts facing each other or around an axis.
- Exact correspondence of form and constituent configuration on opposite sides of a dividing line or plane or about a center or an axis.
Length
Various instruments are used to measure length. For example:
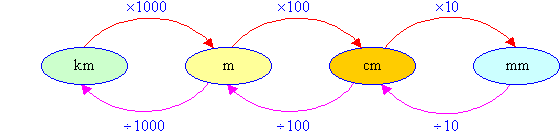
To convert length from a larger unit into a smaller unit, multiply by the relevant power of 10.
To convert length from a smaller unit into a larger unit, divide by the relevant power of 10.
Example.
Convert the following measurements to the units indicated:
a. 7 cm to mm
b. 8 m to cm
c. 9 km to m
Solution:
- Rulers and tape measures are marked in millimetres or centimetres to measure shorter lengths accurately.
- A trundle wheel is used to measure length to the nearest metre. Note that a counter may be attached to the trundle wheel to count metres.
- A car's odometer often measures distance in tenths of a kilometre.
To convert length from a larger unit into a smaller unit, multiply by the relevant power of 10.
To convert length from a smaller unit into a larger unit, divide by the relevant power of 10.
Example.
Convert the following measurements to the units indicated:
a. 7 cm to mm
b. 8 m to cm
c. 9 km to m
Solution:
Whole Number: Division
- In mathematics, especially in elementary arithmetic, division (÷) is an arithmetic operation.
- Another basic view of division is sharing equally.
Example:
Danesse has 3 friends. She has 12 cookies to share with them. How many cookies does each of the four people get?
- Danesse probably shared her cookies by saying one for you, one for you, so on. Thus the 12 cookies are shared equally by four people, and each gets three cookies.
- Or, you might say that the 12 cookies have been partitioned into four sets of the same size.
Exercises:
- 21 ÷ 3 = ________
- 24 ÷ 4 = ________
- 42 ÷ 7 = ________
- 32 ÷ 8 = ________
- 24 ÷ 8 = ________
- 54 ÷ 6 = ________
- 72 ÷ 6 = ________
- 27 ÷ 9 = ________
- 72 ÷ 9 = ________
- 56 ÷ 7 = ________
Fractions
- A fraction is a number that is written in the form:
- The a is the numerator, and the b is the denominator.
- The line separating the numerator and denominator is a fraction bar.
- Fractions are used when representing numbers that describe the parts of a whole. The fraction a/b also can be read as "a out of b" ,"a over b" or "a divided by b."
- Both a and b must be integers, meaning positive and negative whole numbers.
- The denominator, or b, cannot be zero. This is because one cannot divide by zero.
Example:
If there are 18 students in a classroom, and 6 of the students wear glasses, what fraction of the students wear glasses?
- A fraction can be thought of as "a out of b."
- Total number of students is 18.
- Number of students with glasses is 6.
- Number of students with glasses out of the whole class is 6/18.
Whole Numbers: Multiplication
- Multiplication (often denoted by the cross symbol "×") is the mathematical operation of scaling one number by another.
- Whole-number products greater than 1 can be computed by repeated addition;
- 7 multiplied by 3 (often said as "7 times 3") can be calculated by adding 7 copies of 3 together: 7 x 3 = 3 + 3 + 3 + 3 + 3 + 3 + 3 = 21
- Here 7 and 3 are the "factors" and 21 is the "product".
- 7 multiplied by 3 can also be calculated by adding 3 copies of 7 together: 7 x 3 = 7 + 7 + 7 = 21
Exercises:
- 7 x 1 =
- 6 x 5 =
- 7 x 8 =
- 3 x 9 =
- 6 x 6 =
- 9 x 8 =
- 5 x 7 =
- 6 x 9 =
- 2 x 8 =
- 9 x 9 =
Whole Number : Subtraction
How to subract number:
Example: 99876 -57894 = ?
9|9|8|7|6|
- 5|7|8|9|4|
________
8 17 17
9|9|8|7|6|
- 5|7|8|9|4|
4 1 9 8 2
Exercises:
Example: 99876 -57894 = ?
- Line up the numbers:
9|9|8|7|6|
- 5|7|8|9|4|
________
- Subtract the numbers starting from place value ones to ten thousands:
8 17 17
9|
- 5|7|8|9|4|
4 1 9 8 2
Exercises:
- 203 - 35 =
- 72 - 16 =
- 2180 - 726 =
- 62731 - 12735 =
- 7261 - 3815 =
- 92 - 25 =
- 18 - 10 =
- 8271 - 941 =
- 51426 - 903 =
- 6251 - 170 =
Whole Numbers: Addition
First, we need to work on place values:
45 971
| | | | |___ Ones 1's
| | | |____ Tens 10's
| | |_____ Hundreds 100's
| |_______Thousands 1 000's
|_________Ten Thousands 10 000's
If we expand this out, we get:
45971 = 40 000 + 5 000 + 900 + 70 + 1
Write this from up to down:
4|0|0|0|0|
|5|0|0|0|
|9|0|0|
|7|0|
+ |1|
4 5 9 7 1
How to add up numbers:
Example: 53 681 + 7927 = ?
+ |7|9|2|7|
________
5|3|6|8|1|
+ |7|9|2|7|
6 1 6 0 8
45 971
| | | | |___ Ones 1's
| | | |____ Tens 10's
| | |_____ Hundreds 100's
| |_______Thousands 1 000's
|_________Ten Thousands 10 000's
If we expand this out, we get:
45971 = 40 000 + 5 000 + 900 + 70 + 1
Write this from up to down:
4|0|0|0|0|
|5|0|0|0|
|9|0|0|
|7|0|
+ |1|
4 5 9 7 1
How to add up numbers:
Example: 53 681 + 7927 = ?
- Line up the numbers:
+ |7|9|2|7|
________
- Add up the numbers starting from place value ones to ten thousands:
5|3|6|8|1|
+ |7|9|2|7|
6 1 6 0 8
Whole Numbers
Whole Numbers
Counting Numbers
Natural Numbers
Place Value till Ten Thousands
Place (underlined) Name of Position
1 000 Ones (units) position
1 000 Tens
1 000 Hundreds
1 000 Thousands
10 000 Ten Thousands
1 000 000 Hundred Thousands
1 000 000 Millions
Place Value
Example
The number 21,040:
- Whole Numbers are simply the numbers 0, 1, 2, 3, 4, 5, … (and so on)
No fraction!
Counting Numbers
- Counting Numbers are Whole Numbers, but without the zero. Because you can't "count" zero. So they are 1, 2, 3, 4, 5, … (and so on).
Natural Numbers
- Mean either "Counting Numbers" {1, 2, 3, ...}, or "Whole Numbers" {0, 1, 2, 3, ...}, depending on the subject.
Place Value till Ten Thousands
- The position, or place, of a digit in a number written in standard form determines the actual value the digit represents.
- Below shows the place value for various positions:
Place (underlined) Name of Position
1 000 Ones (units) position
1 000 Tens
1 000 Hundreds
1 000 Thousands
10 000 Ten Thousands
1 000 000 Hundred Thousands
1 000 000 Millions
Place Value
Example
The number 21,040:
- Has a 2 in the ten thousands place,
- a one in the thousands place,
- a 4 in the tens place,
- and a 0 in both the hundreds and ones place.
- Can be written as twenty-one thousand and forty.